da dehnt sich keine Schraube
Mikroskopisch sicherlich, wenn auch nicht im Sinne einer Dehnschraube, die danach nicht mehr in ihre ursprüngliche Form zurückgeht. Sonst könnte man die Radschrauben nicht wiederverwenden.
Stahl ist elastisch und seine Ausdehnung bei wirkender Kraft im nichtverändernden Bereich folgt dem Hookschen Gesetz F=d*s, bzw. S = D/d mit S Dehnstrecke, d Federkonstante (je größer, desto härter der Stahl als "Feder") und F die Dehnkraft auf den Stahl.
Deswegen haben normale Schrauben auch eine Zugfestigkeit und Streckgrenze angegeben. Zugfestigkeit ist die maximale Kraft in Newton, die die Schraube aushalten kann und die Streckgrenze ist der Anteil davon, den sie das reversible (also ohne dauerhafte Dehnung) aushält.
Z.B. der Aufdruck 8.8 bedeutet, die Schraube hält 800N aus (erste Zahl) und 80% davon (Zweite Zahl; => 640N) kann sie ohne bleibenden Folgen gedehnt werden.
Mehr dazu zum Beispiel hier:
Festigkeitsklasse von Schrauben
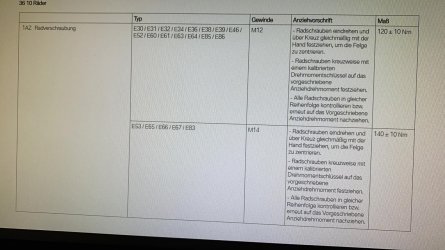
Nebenbei: Man darf natürlich nicht die Zugkraft und das Anzugsdrehmoment miteinander vertauschen. Das Drehmoment bewirkt zwar durch das Gewinde eine Zugkraft, aber da spielt noch Reibung und Gewindesteigung eine Rolle. Mit Öl auf dem Gewinde zum Beispiel ist die Reibung viel geringer, die man für eine gewisse Zugkraft braucht. Und dann zieht man trotzdem mit 120NM an (oder handfest
) und die Schraube reißt ab, weil nun statt der 500N Zugkraft plötzlich z.B. 1000N Zugkraft wirken.
