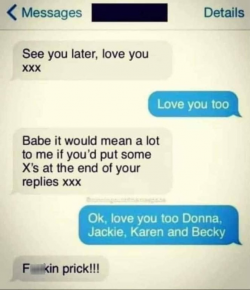
Witze an die Sonne!
- Ersteller chris22
- Erstellt am
Lippe
macht Rennlizenz
Lippe
macht Rennlizenz
Lippe
macht Rennlizenz
Lippe
macht Rennlizenz
Isoklinker
Performance Monster
Snow-White
Orange - nicht Rot!
Und wie hat sie ihn nun ihm gegeben?
Tim
(Der über Witze nicht lachen kann, in denen Rechtschreibfehler stecken)
…. boah ! Der Aufgabensteller kennt das Dreieck des Pythagoras auch nicht wirklich - oder ist 4 jetzt kleiner als 3 ? - Da wundert man sich, dass die Blagen dann auf der Straße kleben.
Kenne ich auch nicht, nur den Satz des Pythagoras.
Da sage ich nur:Tim
(Der über Witze nicht lachen kann, in denen Rechtschreibfehler stecken)
Bist aber auch pingelig!
…. boah ! Der Aufgabensteller kennt das Dreieck des Pythagoras auch nicht wirklich - oder ist 4 jetzt kleiner als 3 ? - Da wundert man sich, dass die Blagen dann auf der Straße kleben.
… naja, das Dreieck hat die Kantenlängen 3, 4 und 5 m (oder andere Längeneinheiten). In „m“ findet es Anwendung auf dem Bau, wenn man einen rechten Winkel anlegen möchte. Da kommt der Begriff „Dreieck des Pythagoras“ her, denn mit dem Lehrsatz kommt der Bauarbeiter nur bedingt klar.Kenne ich auch nicht, nur den Satz des Pythagoras.
Ja, ich meinte das doch auch nur als Scherz, alles gut.
Da ich fast 40 Jahre lang beruflich als Dipl.-Ing. Bauingenieurwesen tätig war ist mir selbiges auch bekannt.
….
Da ich fast 40 Jahre lang beruflich als Dipl.-Ing. Bauingenieurwesen tätig war ist mir selbiges auch bekannt.
… ein Kollege
… jetzt schreib nicht, dass Du in 1984 an der Ruhr Universität Bochum Deine Dipl.-Arbeit geschrieben hast.
Zuletzt bearbeitet:
Nein, Studienbeginn WS 1981, Dipl. Arbeit fertig Februar 86 an der HTW des Saarlandes (damals hieß sie noch FHS)
Eck
The Kabanator
- Registriert
- 3 April 2006
Leute, es gibt hier eine ganze Reihe von Problemen. Es geht ja schon damit los, dass x! gesucht ist und nicht x.
Außerdem geht aus der Aufgabenstellung nicht hervor, dass es sich um ein rechtwinkliges Dreieck handeln soll.
Wenn die Aufgabe korrekt gescannt wurde, handelt es sich ja nicht mal um ein Dreieck, denn wenigstens die linke Kante ist gekrümmt.
